[알고리즘] 6가지 Sorting
Basic Sorting problems 총 6가지를 알아보자.
- Insertion Sort
- Merge Sort
- Bubble Sort
- Selection Sort
- Heap Sort
- Quick Sort
1. Insertion sort
2번째 index 부터 비교를 시작한다. 자신보다 낮은 index 값에 있는 value가 자신의 value 보다 크다면 자리를 바꿔주는 알고리즘이다. 아래 그림과 같이 insertion sort가 진행된다.
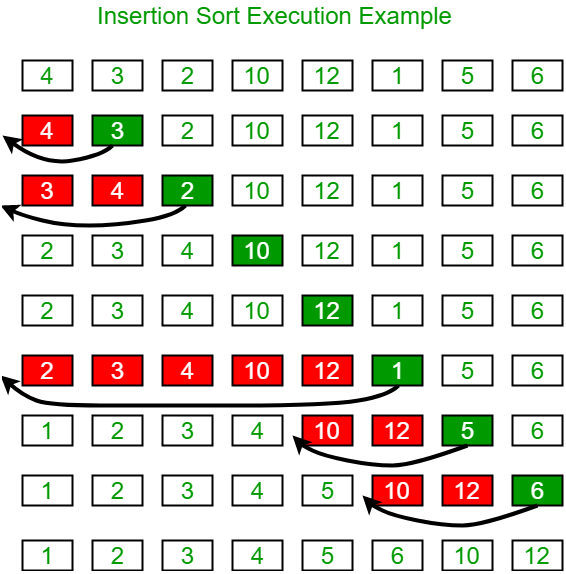
이를 python으로 작성하면 다음과 같다.
def insertionSort(A,n): # A list, n length of list
for i in range(1,n): # from index 1 to n-1
key = A[i] # keep value A[i] in key
j = i-1 # let j be i-1
while j >= 0 and A[j] > key: # for j >=0 and A[j] > key do while loop
A[j+1] = A[j] # switch value
j -= 1 # decrease j
A[j+1] = key # switch value
return A
print(insertionSort([8,2,4,9,3,6],6))
>>> [2, 3, 4, 6, 8, 9]
worst case : List가 반대로 sorting 된 경우 O(n^2)
best case : List 가 이미 sorting 된 경우 O(n)
2. Merge sort
merge sort : split list into individual elements by successively splitting lists into two
리스트를 2개의 독립적인 list으로 반복적으로 나누고 이를 순차적으로 merge 하면서 sorting한다.

worst case : O(nlogn)
python 코드로 작성해보면 다음과 같다.
def mergeSort(A):
n = len(A)
if n<=1:
return A
mid = n//2
group1 = mergeSort(A[:mid]) # recursively merge sort 1st list
group2 = mergeSort(A[mid:]) # recursively merge sort 2nd list
result = []
while group1 and group2: # until group1 and group2 has values left
if group1[0] < group2[0]:
result.append(group1.pop(0))
else:
result.append(group2.pop(0))
while group1:
result.append(group1.pop(0))
while group2:
result.append(group2.pop(0))
return result
print(mergeSort([8,2,4,9,3,6]))
3. Bubble sort
가장 단순한 sorting 알고리즘 중 하나이다.
Procedure :
- list의 첫 index부터 시작한다.
- 높은 value를 가진 index와 interchange
- 이 procedure를 반복
python으로 구현하면 다음과 같다.
def bubbleSort(a):
n = len(a)
if n == 1:
return a
for i in range(n):
for j in range(i+1,n):
if a[i] > a[j]:
temp = a[j]
a[j] = a[i]
a[i] = temp
return a
print(bubbleSort([8,2,4,9,3,6]))worst : O(n^2)
best : O(n)
4. Selection sort
반복적으로 최소값을 찾아가면서 array를 sorting한다.
이 알고리즘은 2가지 subarray를 가지는데. 하나는 sorting이 완료된 subarray, 하나는 sorting이 완료되지 않은 array이다.
Unsorted subarray에서의 가장 최소값은 sorted subarray로 가게된다.
python으로 구현하면 다음과 같다.
def selectionSort(a):
for i in range(len(a)-1):
min_idx = i
for j in range(i+1, len(a)):
if a[j] < a[min_idx]:
min_idx = j
a[i], a[min_idx] = a[min_idx], a[i]
return a
worst case : O(n^2)
5. Heap sort
Binary Heap data 구조를 이용한 comparison-based sorting이다.
먼저 input array를 max heap 형태로 바꾸어준다. 이때 가장 큰 값은 root node에 존재하게 된다.
Last item과 root node(최대값)을 바꾸고 size를 1개 줄여준다.
다시 tree를 heapify 해준다. Max heap 형태로 바꾸어준다
위 과정들을 heap size가 1보다 커질때까지 반복한다.
Q. Complete binary tree?
Complete binary tree는 parnet node가 2개의 child node보다 큰/ 작은 tree를 말한다. 전자는 max heap, 후자는 min heap이라고 부른다.

이를 python으로 구현하면 다음과 같다.
6. Quick sort
Quick sort는 array 안에있는 element를 하나 골라 pivot으로 정한다. 정한 piveot 을 기준으로 pivot보다 작은 값들을 pivot의 왼쪽으로, pivot보다 큰 값들을 오른쪽으로 정렬하여 sorting을 하는 방식이다. 그리고 이를 계속 recursive하게 반복한다.
Pivot을 정하는 기준은 여러가지이다.
- pick first element as pivot
- pick last element as pivot
- pick rondom element as pivot
- pick median as pivot
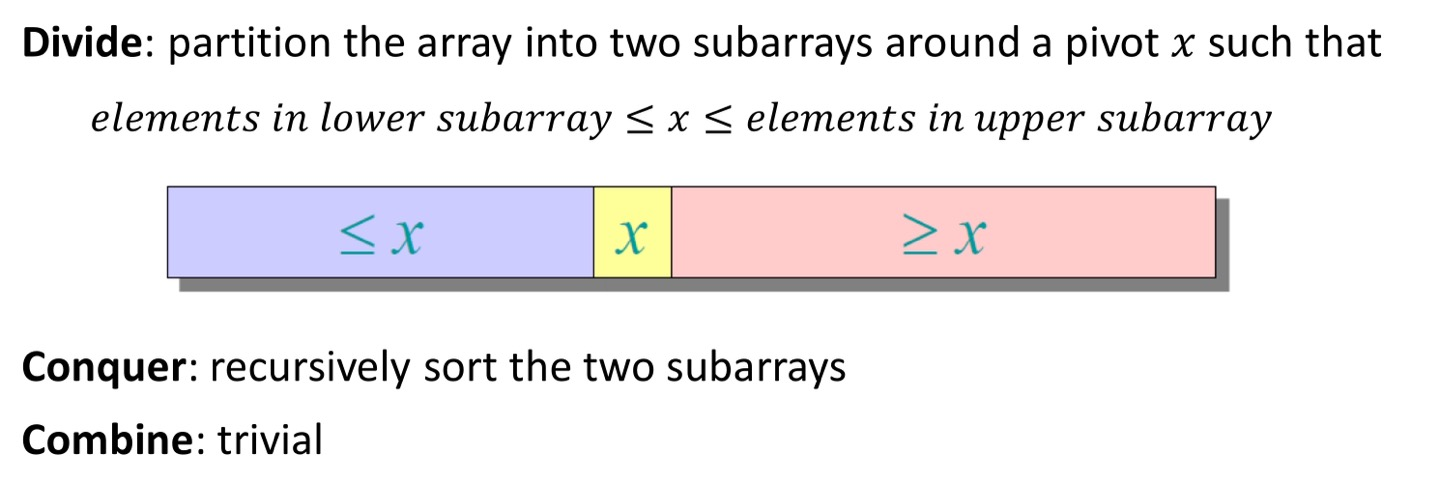
python으로 구현하면 다음과 같다.
# quick sort
def partition(A,p,q): # p start index, q last index
pval = A[p]
pidx = p # pivot index
for i in range(p+1,q): #왼쪽
if A[i] <= pval:
pidx +=1 # pivot idx plus 1
A[pidx], A[i] = A[i], A[pidx] # swap value of i and pidx ( small value next to pivot )
A[p],A[pidx] = A[pidx], A[p] # change pivot
# return pivot index
return pidx
def Quicksort(A,p,r):
if p < r : # p : start position of A, q : end position of A
q = partition(A,p,r) # left right 나누기
#recursive
Quicksort(A,p,q) #left
Quicksort(A,q+1,r) #right
return A
A=[8,9,1,5,4,6,3,7]
print(Quicksort(A,0,len(A)))
>>> [1,3,4,5,6,7,8,9]
worst : O(n^2)
best : when it picks the middle element as pivot O(nlgn)
Summary of Algorithms
| Best | Average | Worst | Space complexity | |
| Bubble Sort | O(n) | O(n^2) | O(n^2) | O(1) |
| Insertion Sort | O(n) | O(n^2) | O(n^2) | O(1) |
| Merge Sort | O(nlgn) | O(nlgn) | O(nlgn) | O(n) |
| Selection Sort | O(n^2) | O(n^2) | O(n^2) | O(1) |
| Heap Sort | O(nlgn) | O(nlgn) | O(nlgn) | O(1) |
| Quick Sort | O(nlgn) | O(nlgn) | O(n^2) | O(lgn) |
계속 작성중...